Constitutive Modelling of Fibre Networks with Stretch Distributions

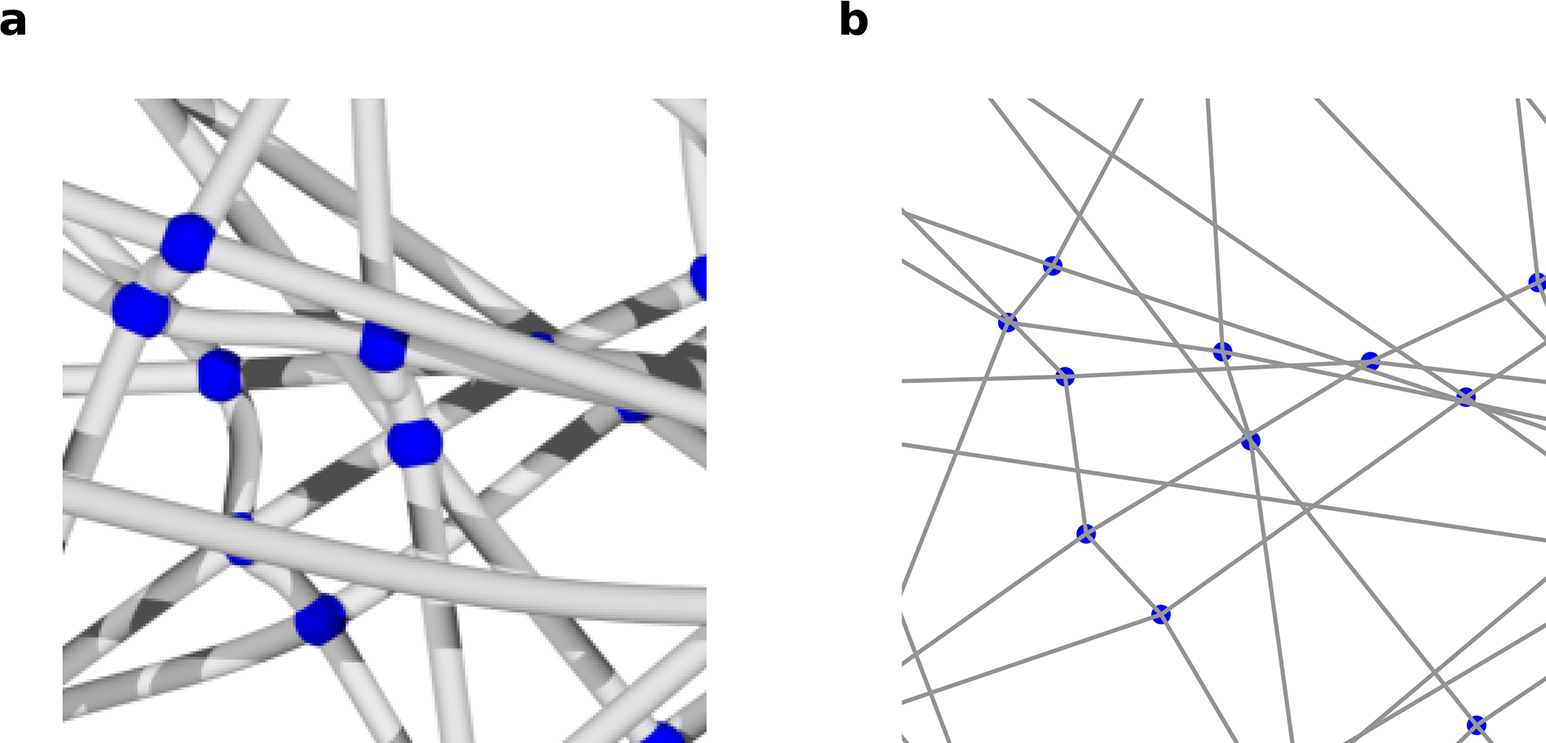
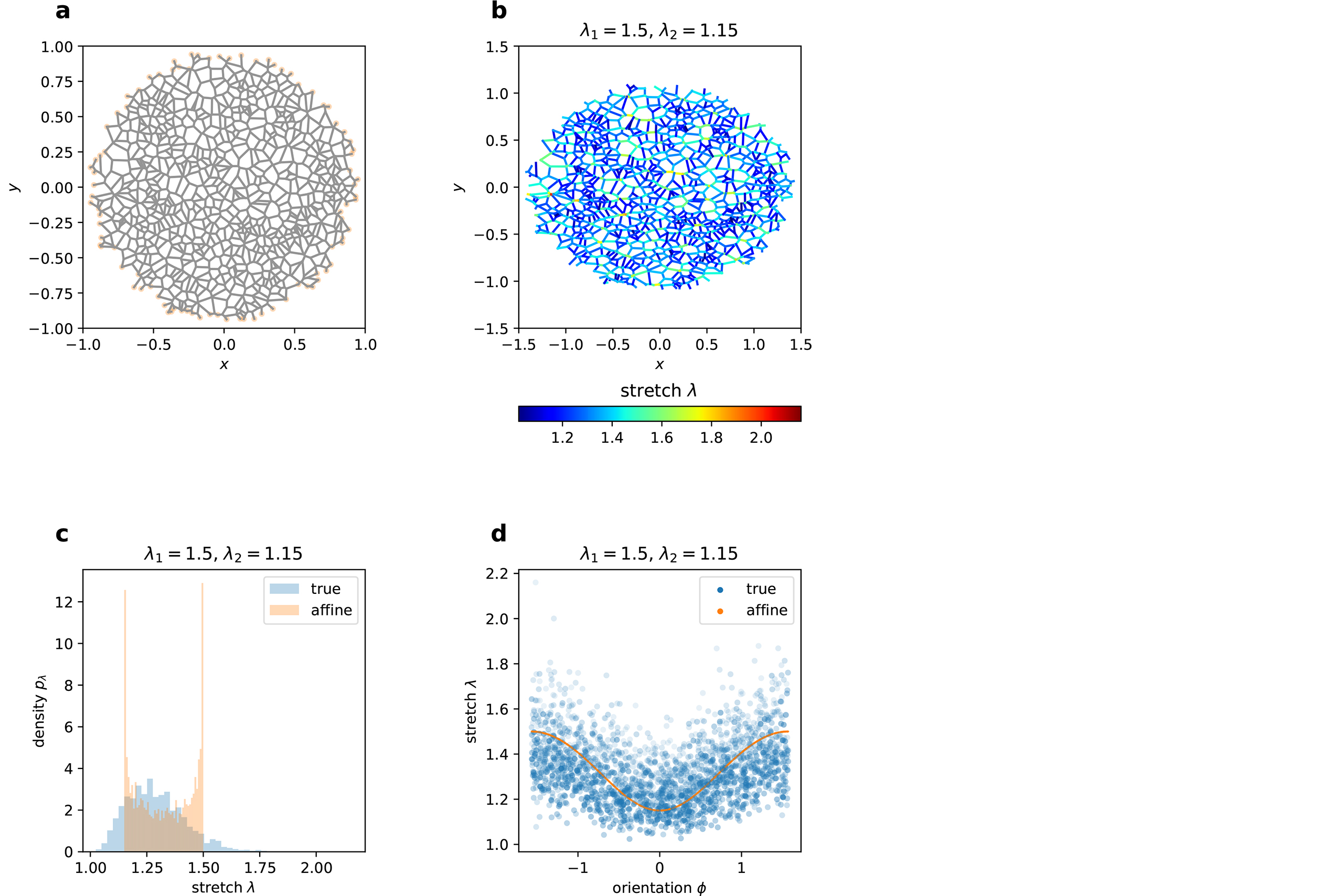
The random fibre network characteristics result from the network structure and the individual fibre material properties. Discrete network models to simulate these materials employ numerical multi-scale simulations with a finite amount of connected fibres (Fig. 1, Fig. 2) and subsequent homogenisation or averaging procedures [2]. Due to the statistical background of these simulations, the generalisability of the corresponding results is often difficult or limited, and additionally, the associated computational costs are high. Analytical approaches are based on physically motivated continuum mechanical models. Here, a constitutive assumption that relates the micro-kinematics of the single fibres with the macroscopic deformations of the network replaces simulations with discretised networks. While this approach is favourable with regard to computational costs, it is prone to oversimplifying the mechanisms responsible for the scale transition. Indeed, comparing the micro-kinematics revealed in multi-scale simulations and those stemming from common continuum mechanical models reveals large discrepancies (Fig. 2c) [3, 4]. This highlights the need to reevaluate and reformulate the assumptions that govern the macro to micro transitions.

A new two-scale approach to network modelling

The new approach for constitutive modelling of random fibre networks generally applies to non-affine fibre kinematics and includes affinity as a special case. Instead of defining the motion of a single fibre depending on its initial spatial orientation, the method developed here focuses on finding the probability distributions of energetically relevant quantities, such as the fibre stretch, within the random fibre network. In a central force network, the average fibre energy can be calculated from the fibre stretch distribution (on the micro-scale) and is proportional to the network’s total energy (on the macro-scale). The modelling approach bridges the macro and micro scale and introduces an entire new space for constitutive modelling.

New Perspectives and Implementations concerning the affine Deformation

Despite its generally non-affine applicability, the novel approach provides a new perspective on affine microsphere models [5]. The associated integration of constitutive equations over the surface of the 2- or 3-dimensional unit sphere has been used as an averaging method in many branches of physics and engineering, including continuum mechanics. It is, e.g., the basic ingredient of the microsphere and full-network models for rubber-like materials [5] and the structural approach in biomechanics [6].

Only in few cases, the integral can be solved analytically so that, typically, quadrature is employed. If the integrand can be expressed as a finite power series, an invariant-based analytical integration can be performed, leading to an invariant-representation of the constitutive equations [7].

However, in many cases relevant to the mechanics of soft materials, the integrands are not analytic, e.g. due to piecewise definitions or asymptotic behaviour.

With the new approach the domain of integration changes from the sphere (orientations) to the reals (stretches) (Fig. 3). For the special case of the affine microsphere, the domain is bounded between the minimum and maximum (squared) principal stretch.  

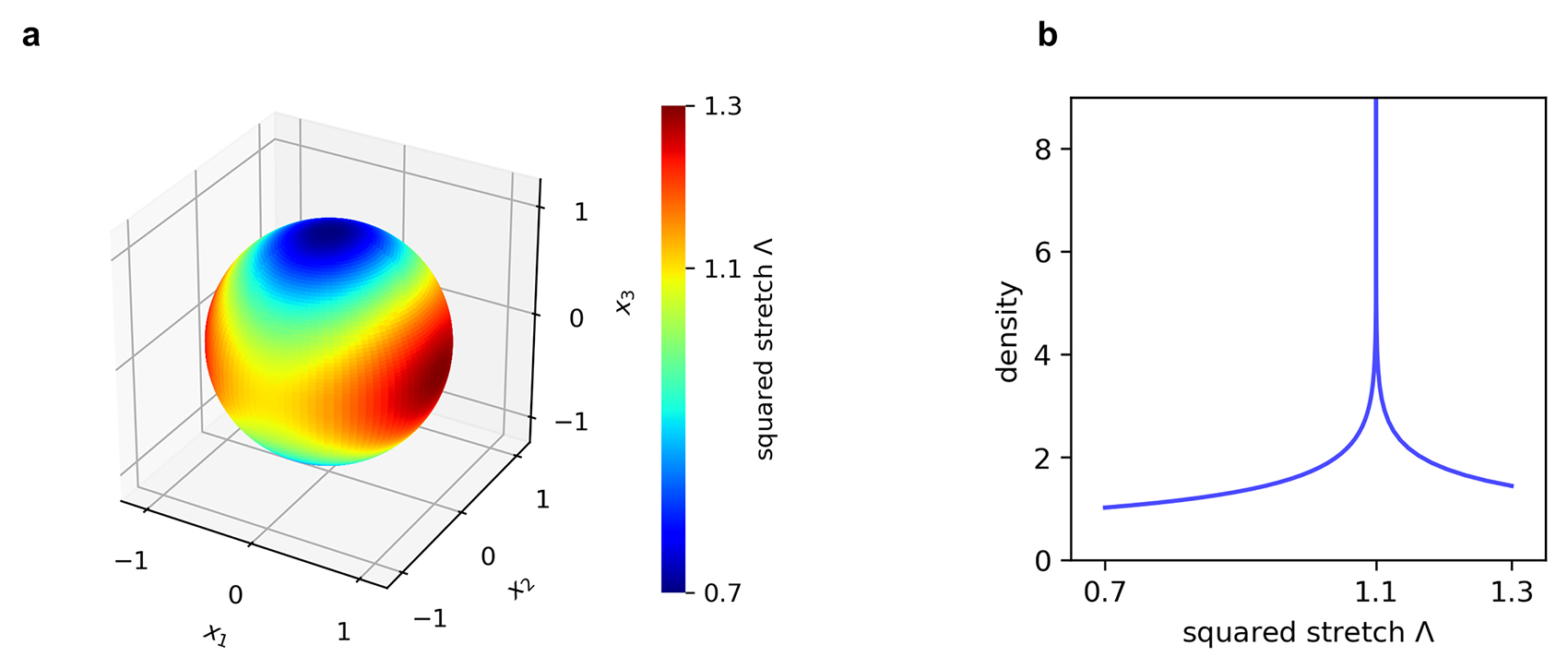
Non-affine two scale model

Multi-scale mechanical models allow to infer microscopic information from the macroscopic response. Two-scale models of fibre network materials are relevant in many fields of engineering, but also in computational mechanobiology problems, where tissue-scale loads are transferred to the cell scale through a collagenous network to provide the cues for various cellular processes [8]. Discrete network models (DNMs) are a common strategy for two-scale problems. DNMs reveal micro-scale information far beyond real experiments and challenge the macro-micro transitions used by the majority of the common continuum mechanical concepts, but also provide the basis to develop novel approaches. One piece of information is the distribution of fibre stretch within the network [8,9,10]. Based on studying various DNM representative volume elements (RVEs) of generally non-linear elastic fibres (Fig. 2 illustrates one example), we propose a constitutive relation between this micro-kinematic distribution and the macroscopic deformation imposed via the boundary conditions. Our analysis revealed a strong resemblance of the obtained stretch histograms with the log-normal distribution L (Fig. 4).

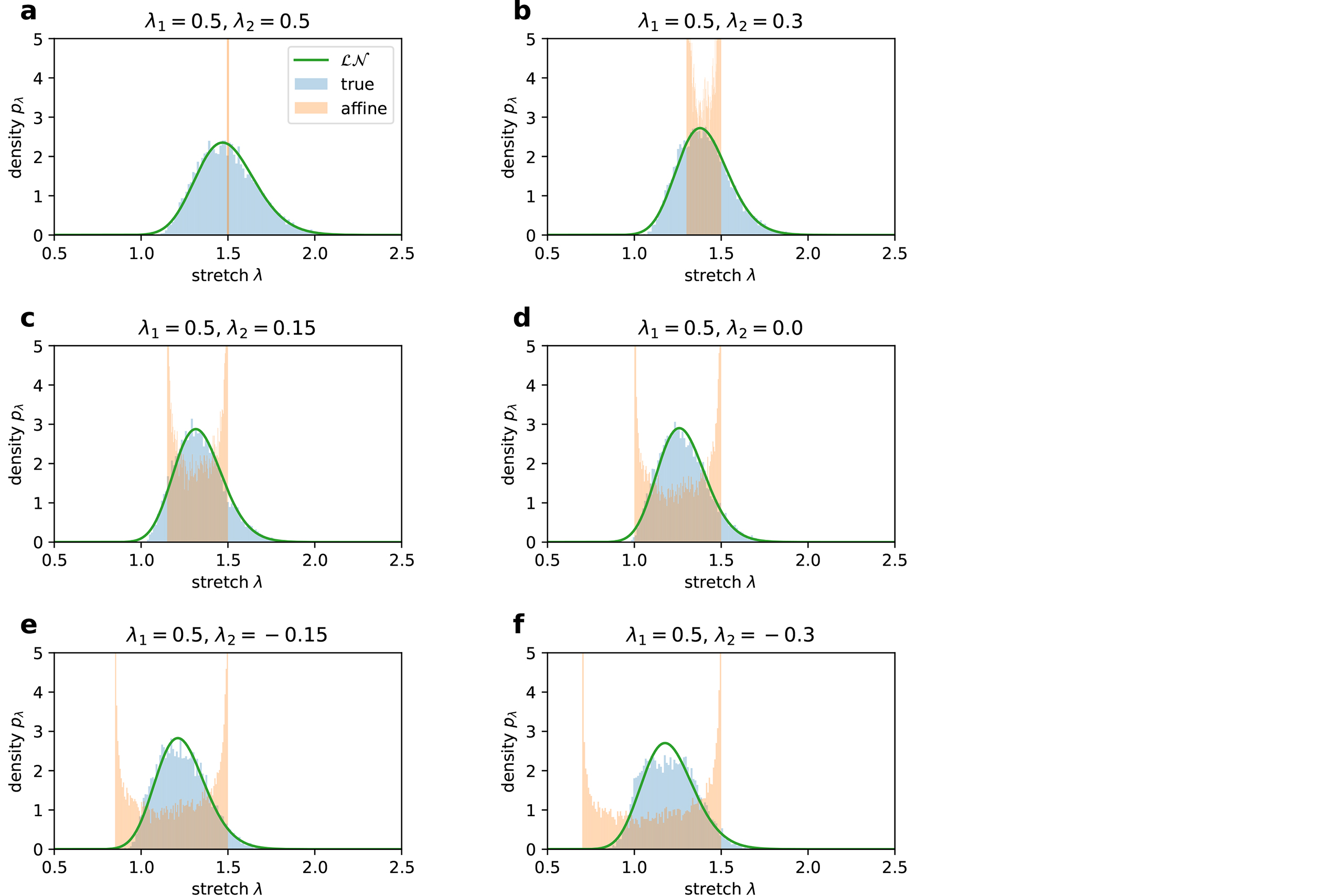
Describing L in terms of the macroscopic deformation, this novel approach yields excellent agreement with the homogenised stress and energetic response of the DNM RVE, and at the same time preserves the micro-kinematic information on the distribution of stretch, making it a promising tool for efficient computational analysis of fibre network materials.

Finally, we develop methods to overcome the costly generation of a numerical DNM ground truth needed to parametrise the model, and sketch strategies to obtain the relevant information for model calibration from real experiments.

Funding

The financial support by the Swiss National Science Foundation (SNF, Project No. 182014) is greatly acknowledged.